Statystyki opisowe to procedury służące porządkowaniu i podsumowywaniu danych, pozwalające uzyskać informacje o najważniejszych charakterystykach danego zbioru (Heiman 2010). Wśród najpopularniejszych statystyk opisowych znajdują się miary tendencji centralnej oraz miary rozproszenia.
Miary tendencji centralnej pozwalają na uzyskanie informacji o najbardziej typowej bądź reprezentatywnej wartości dla populacji (Healey 2011). Do miar tendencji centralnej zaliczamy m.in dominantę (modalną), medianę oraz średnią. Dominanta to najczęściej występująca wartość w zbiorze, mediana to wartość dzieląca zbiór na dwie równe części, zaś średnia arytmetyczna (najpopularniejszy rodzaj średniej) jest ilorazem sumy wartości występujących w zbiorze oraz liczby występujących w nim elementów.
Wykorzystując do opisu danego zbioru (np. określonej próby) miary tendencji centralnej, badacz powinien pamiętać o ograniczeniach związanych poziomem pomiaru zmiennej wykorzystywanej w analizach. Wyznaczanie wartości modalnej ma sens już przy zmiennej nominalnej (np. stan cywilny), mediany – przy zmiennej porządkowej (np. poziom wykształcenia), zaś średniej – jedynie przy zmiennych mierzonych na poziomie interwałowym i ilorazowym (np. wiek).
Miary rozproszenia (zmienności, zróżnicowania) pozwalają na uzyskanie informacji o tym, jak bardzo różnią się od siebie wartości w obrębie danego zbioru (por. Heiman 2010). Najczęściej wykorzystywanymi miarami rozproszenia są: rozstęp, wariancja oraz odchylenie standardowe. Wykorzystanie którejkolwiek z nich ma sens, gdy dysponujemy zmiennymi na skali interwałowej lub ilorazowej. Rozstęp to różnica pomiędzy największą a najmniejszą wartością w zbiorze. Bardziej skomplikowanym procesem jest wyliczenie wartości wariancji oraz bazującej na niej wartości odchylenia standardowego. Wariancję w populacji obliczamy z wzoru: 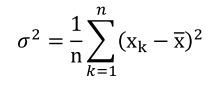 Wariancja jest sumą podniesionych do kwadratu różnic pomiędzy poszczególnymi wartościami występującymi w zbiorze a średnią, podzieloną przez liczbę występujących w zbiorze wartości. Wariancja to zatem średni kwadrat odchylenia wartości od średniej (por. Górniak, Wachnicki 2004: 153). Wartość odchylenia standardowego to z kolei pierwiastek kwadratowy z wartości wariancji:
Wariancja jest sumą podniesionych do kwadratu różnic pomiędzy poszczególnymi wartościami występującymi w zbiorze a średnią, podzieloną przez liczbę występujących w zbiorze wartości. Wariancja to zatem średni kwadrat odchylenia wartości od średniej (por. Górniak, Wachnicki 2004: 153). Wartość odchylenia standardowego to z kolei pierwiastek kwadratowy z wartości wariancji: 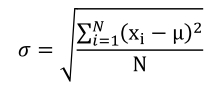 Im mniejsza wartość odchylenia standardowego, tym wartości zmiennej są bardziej zbliżone do wartości średniej, im jest ona większa, tym są one od niej bardziej oddalone. Odchylenie standardowe często interpretuje się potocznie jako średni rozrzut wokół średniej. Nie jest to określenie precyzyjne (taka interpretacja przysługuje odchyleniu przeciętnemu), jednak w przybliżeniu oddaje sens tej nieco abstrakcyjnej miary (Górniak, Wachnicki 2004). Przykładowo: jeśli odchylenie standardowe miesięcznego wynagrodzenia wynosi 700 zł, a średnia 3600 zł możemy te wartości interpretować w następujący sposób: miesięczne dochody osób w tej populacji średnio różniły się od 3600 zł o 700 zł.
Im mniejsza wartość odchylenia standardowego, tym wartości zmiennej są bardziej zbliżone do wartości średniej, im jest ona większa, tym są one od niej bardziej oddalone. Odchylenie standardowe często interpretuje się potocznie jako średni rozrzut wokół średniej. Nie jest to określenie precyzyjne (taka interpretacja przysługuje odchyleniu przeciętnemu), jednak w przybliżeniu oddaje sens tej nieco abstrakcyjnej miary (Górniak, Wachnicki 2004). Przykładowo: jeśli odchylenie standardowe miesięcznego wynagrodzenia wynosi 700 zł, a średnia 3600 zł możemy te wartości interpretować w następujący sposób: miesięczne dochody osób w tej populacji średnio różniły się od 3600 zł o 700 zł.
Magierowski M. Statystyki opisowe. Dostępny: http://www.researchonline.pl/baza?podkategoria=25, data dostępu: .././../2013.
Górniak J., Wachnicki J. 2004. Pierwsze kroki w analizie danych. Kraków: SPSS Polska.
Heiman G. W. 2010. Basic Statistics for the Behavioral Sciences. Cengage Learning.
Healey J. 2010. Statistics: a Tool for Social Research. Cengage Learning.
100 000+
Zrealizowanych ankiet. Dołącz do grona naszych klientów!